Probabilidad
En los fenómenos aleatorios, el conjunto de resultados ( \(\Omega\) ) define todas las formas en las que se puede manifestar un fenómeno (el espacio muestral).
| Moneda | \(\Omega = \{cara, cruz\}\) |
| Dado | \(\Omega = \{1,2,3,4,5,6\}\) |
La probabilidad de que ocurra algo perteneciente al conjunto de resultados es siempre 1.
| Notación | Conjunto | Suceso |
|---|---|---|
| \(\Omega\) | conjunto de resultados | \(P(\Omega) = 1\) (“suceso seguro”) |
| \(\emptyset\) | conjunto vacío | \(P(\emptyset) = 0\) (“suceso imposible”) |
Sucesos y subconjuntos
Los sucesos ( \(\omega\) ) son resultados posibles del experimento aleatorio. Un suceso equivale a un sub-conjunto de \(\Omega\) (espacio muestral).
El suceso obtener un número impar en un dado sería el subconjunto \(I\), que se anotaría como \(\{1,3,5\}\).
Complementario
El complementario de un evento también es un evento; es la probabilidad de que no ocurra.
La cuota, momio u odds indica cuanto más frecuente es que un fenómeno ocurra que lo contrario:
\[ \dfrac{P(E)}{P(E^{\complement})} \]
Unión
La unión define el conjunto en el que ocurre el evento A y/o B (ambos subconjuntos dentro del espacio muestral).
Dado un espacio \(S = \{1,2,3,4,5,6\}\) donde los números impares se definen como \(A = \{1,3,5\}\) y los números <4 como \(B = \{1,2,3\}\) :
\[ A \cup B = \{1,2,3,5\} = \dfrac{4}{6} \]
Intersección
La intersección define el conjunto en el que ocurren A y B al mismo tiempo:
\[ A \cap B = \{1,3\} \]
Probabilidad conjunta
No es la suma de las probabilidad de cada conjunto, porque esto obviaría que algunos elementos están en ambos. La probabilidad real sería la suma de los conjuntos por separado, menos una instancia de los duplicados (utilizando la intersección):
\[ P(A \cup A) = P(A) + P(B) - P(A \cap B) \]
Eventos mutuamente excluyentes
Son aquellos eventos en los que, dado uno, el otro no puede haber ocurrido:
\[ P(A \cap B) = P(\emptyset) = 0 \]
y por tanto
\[ P(A \cup B) = P(A) + P(B) \]
Probabilidad condicional
Es la probabilidad de que el evento A ocurra dado que ha ocurrido el evento B
\[ P(A|B) = \dfrac{P(A \cup B)}{P(B)} \]
Los complementarios siguen funcionando en la probabilidad condicional de la misma manera:
\[ P(A|B) = 1 - P(A^{c}|B) \]
Probabilidad total
Reordenando la fórmula de la probabilidad condicional obtenemos
\[ P(A \cup B) = P(A|B) \times P(B) = P(B|A) \times P(A) \]
Con esta fórmula podemos obtener la probabilidad de que ocurra un evento a lo largo de un espacio muestral partido:
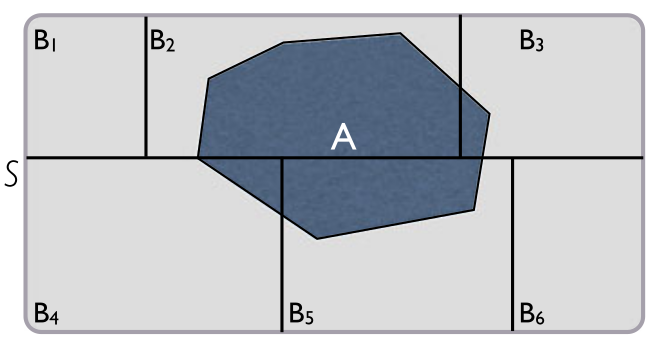
\[ P(A) = \sum_{k=1}^{K}{P(A|B_{k}) \times P(B_{k})} \]
Eventos independientes
Si un evento es independiente, \(P(A|B) = P(A)\); en este caso
\[ P(A \cap B) = P(A) \times P(B) \]
\[ P(A \cup B) = P(A) + P(B) \]
Resumen
| Suceso | Descripción |
|---|---|
| Suceso seguro | \(P(\Omega) = 1\) |
| Suceso imposible | \(P(\emptyset) = 0\) |
| Complementario de un suceso | \(P(E^{c}) = 1 - P(E)\) |
| Suceso implicado | \(P(A) \leq P(B)\) siempre que ocurre A ocurre B |
| Probabilidad | Independientes | Dependientes | Condicional |
|---|---|---|---|
| \(P(A \cap B)\) | \(P(A) \times P(B)\) | \(P(A\vert B) \times P(B)\) | |
| \(P(A \cup B)\) | \(P(A) + P(B)\) | \(P(A) + P(B) - P(A) \times P(B)\) |